In Whitehead (2020) I describe the problems in the DMT (2015) data. It is full of non-monotonicities, flat portions of bid curves and fat tails. A non-monotonicity is when the percentage of respondents in favor of a policy increases when the cost increases. In other words, for a pair of cost amounts it appears that respondents are irrational when responding to the survey. This problem could be due to a number of things besides irrationality. First, respondents may not be paying close attention to the cost amounts. Second, the sample sizes may be simply too small to detect a difference in the correct direction. Whatever the cause, non-monotonicities increase the standard errors of the slope coefficient in a parametric model.
Flat portions of the bid curve exist when the bid curve may be downward sloping but the slope is not statistically different from zero. This could be caused by small differences in cost amounts and/or it is due to sample sizes that are too small to detect a statistically significant difference. For example, there may be little perceived difference between a cost amount of $5 and $10 compared to $5 and $50. And, even if the percentage of responses in favor of a policy is economically different between two cost amounts, this difference may not be statistically different due to small sample sizes.
Fat tails may exist when the percentage of respondents who are in favor of a policy is high at the highest cost amount. However, this is only a necessary condition. A sufficient condition for a fat tail is when the percentage of respondents who are in favor of a policy is high at two or more of the highest cost amounts. In this case, the fat tail will cause a parametric model to predict a very high cost amount that drives the probability that respondents are in favor of a policy to (near) zero. A fat tail will bias a willingness to pay estimate upwards because much of the WTP estimate is derived from the portion of the bid curve when the cost amount is higher than the cost amount in the survey.
DMT (2020) state that these problems also occur in Chapman et al. (2009) and a number of my own CVM data sets. They are correct. But, DMT (2020) are confusing the existence of the problem, in the case of non-monotonicity and flat portions, with the magnitude of the problem. And, they are assuming that if the necessary condition for fat tails exists then the sufficient condition also exists. Many, if not most, CVM data sets will exhibit non-monotonicities and flat portions of the bid curve. But, these issues are not necessarily an empirical problem. The extent of the three problems in DMT (2015) is severe — so severe that it makes their attempt to conduct an adding up test (or any test) near impossible.
To prove this to myself I estimated the logit model, WTP value and 95% Krinsky-Robb confidence intervals for 20 data sets. Five of the data sets are from DMT (2015), 2 are from Chapman et al. (2009) and 13 are from some of my papers published between 1992 and 2009 (DMT (2020) mention 15 data sets but two of the studies use the same data as in another paper). The average sample size for these 20 data sets is 336 and the average number of cost amounts is 5.45. The average sample size per cost amount is 64, which is typically sufficient to avoid data quality problems (a good rule of thumb is that the number of data points for each cost amount should be n > 40 in the most poorly funded study).
These averages obscure differences across study authors. The average sample size for the DMT (2015) data sets is 196. With 6 cost amounts the average sample size per cost amount is 33. The Chapman et al. (2009) study is the best funded and the two sample sizes are 1093 and 544. With 6 cost amounts the sample sizes per cost amount are 182 and 91. The Whitehead studies have an average sample size of 317 and with an average of 5 cost amounts, the sample size per cost amount is 65 (the variance of these means are large). Already, differences across these three groups of studies emerge.
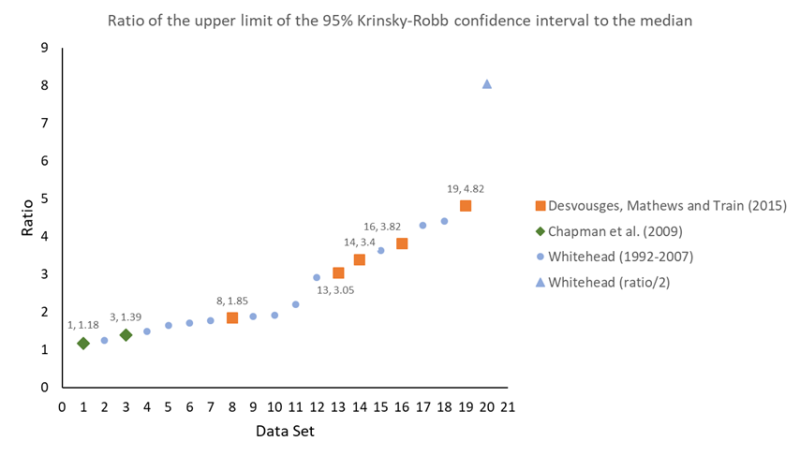
There are a number of dimensions over which to compare the logit models in these studies. My preferred measure is the ratio of the upper limit of the 95% Krinsky-Robb confidence interval for WTP to the median WTP estimate. This ratio will be larger the more extensive is the three empirical problems mentioned above. As this problem worsens, hypothesis testing with the WTP estimates (again, a function of the the ratio of coefficients) becomes less feasible. It is very difficult to find differences in WTP estimates when the confidence intervals are very wide. To suggest that this measure has some validity, the correlation between the ratio and the p-value on the slope coefficient is r = 0.96.
The results of this analysis are shown below. The ratio of the upper limit of the confidence interval to the median is sorted from lowest to highest. The DMT (2015) values are displayed as orange squares, the Chapman et al. (2009) values are displayed as green diamonds and the Whitehead results are displayed as blue circles and one blue triangle. The blue triangle is literally “off the chart” so I have divided the ratio by 2. This observation, one of three data sets from Whitehead and Cherry (2007), does not have a statistically significant slope coefficient.
Considering the DMT data, observation 19, with a ratio of 4.82 (i.e., the upper limit of the K-R confidence interval is about 5 times greater than the median WTP estimate), is the worst data set. Observation 8, the best DMT data set, has their largest sample size of n=293. The Chapman et al. (2009) data sets are two of the three best in terms of quality. The Whitehead data sets range from good to bad in terms of quality. Overall, four of the five DMT data sets are in the lower quality half of the sample (defined by DMT*).
Of course, data quality should also be assessed by the purpose of the study. About half of the Whitehead studies received external funding. The primary purpose of these studies was to develop a benefit estimate. The other studies were funded internally with a primary purpose of testing low stakes hypotheses. In hindsight, these internally funded studies were poorly designed with sample sizes per bid amount too small and/or poorly chosen bid amounts. With the mail surveys the number of bid amounts was chosen with optimistic response rates in mind. With the A-P sounds study a bid amount lower than $100 should have been included. Many of the bid amounts are too close together to obtain much useful information.
In contrast, considering the history of the CVM debate and the study’s funding source (Maas and Svorenčík 2017), the likely primary purpose of the DMT (2015) study is to discredit the contingent valuation method in the context of natural resource damage assessment. In that context, the study is very high stakes and, therefore, its problems should receive considerable attention. The DMT (2015) study suffers from some of the same problems that my older data suffers from. The primary problem with the DMT (2015) study is that the sample sizes are too low. It is not clear why the authors chose to pursue valuation of 5 samples instead of 3 to conduct their adding up test (DMT (2012) describe a 3 sample adding up test with the Chapman et al. (2009) study). Three samples may have generated confidence intervals tight enough to conduct a credible test.
In the title of this post I ask “Are the DMT data problems typical in other CVM studies?” This subtitle should really be ‘Are the DMT data problems typical of Whitehead’s CVM data problems in a different era? The survey mode for my older studies was either mail of telephone. Both survey modes were common back in the old days but they have lost favor relative to internet surveys. The reasons are numerous but one is that internet surveys are much more cost-effective and the uncertainty about a response rate is non-existent. Another reason is that internet survey programming is much more effective (with visual aids, piping, ease of randomization, etc). Many of the problems with my old data was due to small sample sizes. This was a result of either poor study design (in hindsight, many CVM studies with small samples should have reduced their bid amounts) or unexpectedly low mail response rates.
It is not clear why DMT (2020) chose to compare their data problems to those that I experienced 15-30 years ago. Unless, in a fit of pique at my comment on their paper, they decided it would be a good idea to accuse me of hypocrisy. I’ve convinced myself that my data compares favorable to the DMT (2015) data. Especially considering the goals of the research. My goals were more modest than testing whether the CVM method passes an adding-up test for which a WTP estimate (the ratio of two regression coefficients) is required (as opposed to considering the sign, sign and significance of a regression coefficient).
*****
*Note that there are more Whitehead data sets than are called out by DMT. I haven’t had time to include all of these into this analysis. But, my guess is that the resulting circles would be no worse than those displayed in the picture below.
Reference
Maas, Harro, and Andrej Svorenčík. ““Fraught with controversy”: organizing expertise against contingent valuation.” History of Political Economy 49, no. 2 (2017): 315-345.